Composing Gloves

The dB and units

Goal

Understand units of pressure, unit conversion and use of the dB in these cases. Also covers Sound Power, Sound Pressure Levels and the inverse square law.

The many different dB scales

There are many dB scales. Each of them for a different purpose. Remember a dB is just a number and without the type of dB given it’s useless. When a dB is used without the proper unit listed to show what reference value was used, we can often use context to figure out what was meant. Giving a dB without a unit is just saying a number.

20 dB increased in the room.

...

20 WHAT? Watts? Ice cream? Pressure? This statement is meaningless. It’s similar to just going up to someone and saying, “I can do 20.” 20 what?!

A better example would be: 20 dB SPL increased in the room.

Units

We will only cover units we need. For a much more complete coverage of units please see appendix E in the book Sound and Synth Basics.

Sound Power

Sound power is the total sound energy emitted by a source. We measure power in Watts. A watt is a joule per second. A joule is a measure of energy.

When energy is applied to cause an object to be displaced we call it work which is also measured in joules, but it’s a sort of “applied joules”. Regular old joules only care about the amount of energy. Work joules care only about the energy that resulted in a displacement, energy that “got stuff done”.

What is a Joule?

A joule is defined as 1 newton of force being applied over one meter. It takes about 1 joule of energy to lift an average apple up a meter. A U.S. gallon of gasoline has about 120 million joules!

So, when we say “the sound power of that speaker is 1 Watt" it means the speaker puts out 1 joule per second of sound energy. Sound energy is not electrical energy, we are saying that the very air is being moved about so violently that an entire Watt of energy is used! This is a very loud sound in terms of sound power because the displacement caused by 1 joule on air particles is massive! A watt of sound power is comparable to a sonic boom!

Note: This is not the measurement speakers use when they say that are 100 Watt speakers. This wattage measurement refers to electrical power and only a small portion of that actually gets translated into particle movement, i.e. sound power. Instead you should look at the speakers sensitivity (which relates electrical power to sound pressure levels).

Sound Power Formula

The formula for sound power is the sound intensity over (meaning multiplied by) an area.

SP=AI SP=A\mathbf{I}
Where SP is sound power, A is area, and I is intensity. \text{Where } SP\text{ is } \allowbreak \text{sound } \allowbreak \text{power, } A\text{ is } \allowbreak \text{area, } \allowbreak \text{and } \mathbf{I}\text{ is } \allowbreak \text{intensity.}

Lets work through what this equation is really saying. To find the sound power of an area simply look at the area and determine the intensity at every point in the area, then add all that up and you get the power meaning the total intensity caused by a source. Intensity is the speed of the particles times the pressure.

The Problem with Sound Power

It's hard to measure. Sound power is concerned with total sound power coming from the source. It doesn’t care about distance from the source.

Picture a sphere surrounding the source. If we were to measure the sound passing through this sphere, then we would have the sound power. If the sphere were to grow or shrink it wouldn’t matter because the amount of sound power would remain the same assuming there is no variable resistance.

However, if you’re sitting in the field and there is a loud speaker making a constant noise you know that the further you get the softer it will get. Why is this? Well, it's because as you get further away the sound will cover a great area. So, it's not that the sound power has disappeared rather the area it’s being spread over has increased! That's one reason why it gets softer. For this reason, we say that intensity level varies inversely (meaning is divided by indicating shrinking) the square of the distance.

Intensity and the Inverse Square Law

Intensity is defined as:

I=pv \mathbf{I} =p\mathbf{v}
Where I is intensity, p is pressure, and v is particle velocity. \text{Where } \mathbf{I}\text{ is } \allowbreak \text{intensity, } p\text{ is } \allowbreak \text{pressure, } \allowbreak \text{and } \mathbf{v}\text{ is } \allowbreak \text{particle } \allowbreak \text{velocity.}

Or using our definition of sound power we can also obtain:

I=SPA \mathbf{I} =\frac{SP}{A}

Using units we can understand what we mean by intensity:

intensity=particle velocitymeterss×pressure Pa intensity=particle\ velocity\frac{meters}{s} \times pressure\ Pa

So if we want to find the intensity of a region we will need a way to determine the sound pressure and particle velocity as each point in the area. We can also make more intuitive sense of "intensity", if there is a high particle speed and a high pressure then its "intense", but if these are low then its not "intense".

The Inverse Square Law

Many things vary with the inverse of some square. Intensity is one of those. If we consider the sound emitting in a free field in all direction we have a sphere.

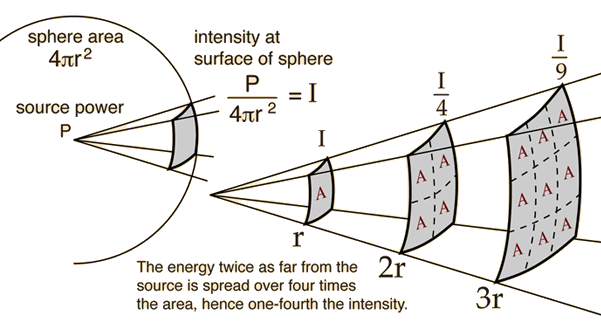
Inverse Square Law

Double click or (ctrl + click) to reset / Mouse wheel to zoom to mouse location / Click + drag to pan view

The surface area of this sphere increases with distance. The power is spread out forming a sphere so we can think of the power as "spreading out" in the shape of a sphere as the sphere emanates outward. The surface area of a sphere is defined by:

4πr2 4\pi r^{2}
. We then take the power and divide it by the area its spread out. This gives:
I=P4πr2 \mathbf{I} =\frac{P}{4\pi r^{2}}
. We see the power is divide by the radius squared or in other words the power varies with the inverse of the square. Hence why it is called the inverse square law.

Ditching Sound Power for Sound Pressure

There are a few problems with sound power:

  1. It is hard to measure.

  1. Your position in the field doesn't matter.

It is hard to measure because in order to actually measure sound power we would need to know the intensity at every point equidistant from the sound source. We could set up microphones all around the source but this would be just a sampling and doing this is not practical in most situations.

Because we care about every point in the field to find the total sound power there is no sense of position. The entire sphere matters, but when we listen to sound where you are listening from can matter a lot! So we need another measure to use.

Sound Pressure Levels

Sound pressure level or SPL can solve this issues. Position will matter and it can be easily measured! Before we can talk about sound pressure levels we need to understand pressure.

Pressure

Pressure is force applied over an area.

P=FA P=\frac{F}{A}
Where P=pressure, F=force, and A=area  \text{Where } P=\text{pressure, } F=\text{force, } \allowbreak \text{and } A=\text{area } \allowbreak \text{}

We can use this definition to find the total force something under pressure experiences:

F=AP F=AP

Common units of pressure are the pascal, torr and atmosphere. In sound we typically use the pascal for reasons that will become clearer as we continue.

The Standard Atmosphere

Normal air pressure in the atmosphere at sea level is defined as an atmosphere. In pascals this is 101,325 pascals! This is why we may come up with different units for the same thing we are measuring such as pressure, using pascal's for the pressure at sea level isn’t very convenient. This is also why pascals are considered a “small” unit.

1 atm =101,325 Pa or 1 atm =1,013,250dynescm2 1\ atm\ =101,325\ Pa\ or\ 1\ atm\ =1,013,250\frac{dynes}{cm^{2}}

Atmosphere came about because a unit of pressure was desired that wasn’t dependent on a particular substance. (760 mmHg (760 millimeters of Mercury))

The Pascal

The pascal is an SI (Système international) unit defined as:

1 Pascal = 1 Newtonmeters2 1\ Pascal\ =\ \frac{1\ Newton}{meters^{2}}

A newton is the SI unit for force and is defined as the amount of force needed to move a kilogram (1000 grams) 1 meter every second squared.

The softest sound a human can hear is generally accepted to be

.00002 Pa .00002\ Pa
! (This can also be written as:
20×10−6Pa 20\times 10^{-6} Pa
or
 20μPa \ 20\mu Pa
.) This measurement is done for 1kHz because humans have nonlinear hearing.

1 pascal is 0.000145psi! Again showing how small it is. Despite how small it is compared to other units of pressure human hearing can detect changes far smaller than a pascal! Hence why we use it.

The Dyne

A Dyne is the force required to accelerate a mass of one gram at a rate of one centimeter per second squared. Note the Dyne is a unit of force, not a pressure. This means when using the dyne we must always include the area it is being applied over if we intend to be talking about a pressure.

1dyne=1gram×centimeterseconds2 1dyne=\frac{1gram\times centimeter}{seconds^{2}}
1 newton=105 dynes 1\ newton=10^{5} \ dynes

Why use the dyne? The dyne is useful because it introduces a unit of mass directly. If we know how much a substance is in grams and we measure its movement over time, then it’s easy to get amount of dynes hence its usefulness. The reference level for the softest sound a human can hear at 1kHz in dynes is

.0002 dyncm2 .0002\ \frac{dyn}{cm^{2}}
. Notice that this is a force over an area, where a dyne is merely just a force, this is why a
cm2 cm^{2}
appears, it converts us to a pressure instead of just a force.

Back to Sound Power

Humans can hear from

10−12 10^{-12}
of a watt up to
10 10
W which yields a
1013 10^{13}
range. The
10−12wm2 10^{-12}\frac{w}{m^{2}}
correlates to the hearing thresholds of humans and that is the reference value we use for SP.

Here is the problem. If we put a microphone close then it will be “louder” and if we move back it will be “softer”, so it seems we are not measuring the total sound energy. However, consider that we are also missing all the other points in the space! We are missing the points behind the source, above, below and side to side! So, in order to get a decent sound power reading we will need to measure from several points and to get the exact reading we need to measure all points.

If we pick our environment carefully we can extrapolate from a single point measurement but in most situations we will not have this convince.

While sound power relates to intensity easily we will now look at how it relates to pressure so we can use SPL instead.

Sound Pressure Level

Sound Pressure Level or SPL is the average amplitude pressure squared at a particular point in a sound field. SPL is also related to Intensity Level (IL) by a square which will become important. In fact the square of pressure varies directly with sound intensity.

pressure2∝ Sound Intensity pressure^{2} \varpropto \ Sound\ Intensity

Where the

∝ \varpropto
means varies directly. This is saying that whatever the sound intensity is the pressure at the point will follow what it is doing but in a squared fashion. So if the sound intensity goes up so to will the pressure but it will go up more because it is squared and if the sound intensity goes down so to will the pressure but more so because again its square value is what will vary.

With sound power our position in the sound field did not matter, but with SPL our position in the field matters.

The derivation for the
dBSPL \mathbf{dB_{SPL}}

We have seen the definition for the dB. This definition works fine for power, but to go from power to intensity we will need to introduce the square.

First we use the dB definition:

dB=10log⁡(xxref) dB=10\log\left(\frac{x}{x_{ref}}\right)

Next we introduce the specific type of dB we will be using. We want dB Sound Power or dB SP so we must use the sound power reference which we know is

10−12 10^{-12}
. So we will have some measured number of Watts over the reference for Watts.

dBSP=10log⁡(WWref)=10log⁡(x W10−12W) d B_{SP} =10\log\left(\frac{W}{W_{ref}}\right) =10\log\left(\frac{x\ W}{10^{-12} W}\right)

Here I show it as just the units for Watts and then show we could assign them some number of Watts, in the top it would be the measured number Watts, some number "x" and in the bottom it will be the reference.

Now we can use what we know about pressure and sound intensity. Consider the fact that sound power is defined by and intensity over some area. We know that pressure varies with the intensity squared, so if we jump to use pressure that means we must also be sure to square the values. This allows us to jump to SPL:

dBSPL=10log⁡(Pa2Paref2) d B_{SPL} =10\log\left(\frac{Pa^{2}}{Pa_{ref}^{2}}\right)

For simplicity I will just write them as the units and their respective reference. Now we are using Pascals and have obtain a dB in the form of SPL! However we now have this square to deal with. When the bottom and top of the fraction are raised to a power and that power matches we can instead treat it as if the entire fraction is raised to that power:

dBSPL=10log⁡(PaParef)2 d B_{SPL} =10\log\left(\frac{Pa}{Pa_{ref}}\right)^{2}

The log has a special math property we can use here. Recall that logs take the numbers and arrange them so that multiplications now act like additions. Well, an exponent is like we are multiplying multiple times which to a log is just adding multiple times. Repeated addition is just multiplication, so to a log a power is the same thing as multiplying. This allows us to take the power and put it in front like a multiplication! (The are many other neat things logs can do, this is just one of them.) We now have:

dBSPL=10(2)log⁡(PaParef) d B_{SPL} =10( 2)\log\left(\frac{Pa}{Pa_{ref}}\right)

This simplifies to:

dBSPL=20log⁡(PaParef) d B_{SPL} =20\log\left(\frac{Pa}{Pa_{ref}}\right)

There we have it! The definition for the log for dB SPL. It should be apparent now that any quantity that varies with a Square will have a 20 used in the log equation rather than a 10. Voltage is a good example. The square of Voltage varies with electrical power so electrical power uses 10 where voltage uses 20.

The 6 and 3 dB properties

Whenever a ratio is put into the dB that is 2:1 we will obtain about 6 or 3 dB more depending on if it's the 20 log or 10 log equation. We could find this for other ratios but we care more about 2:1 since doubling or halving something occurs often.

For example consider 4:2. Plugging in this ratio we get:

dBSPL=10log⁡(42)≈3 dB_{SPL} =10\log\left(\frac{4}{2}\right) \approx 3
dBSPL=20log⁡(42)≈6 dB_{SPL} =20\log\left(\frac{4}{2}\right) \approx 6

This will hold for any ratio of double, you could plug in 200 to 400 or 5000 to 10000, they will produce 3 for the 10 log equation and 6 for the 20 log. If you are using dB for something that is related by a square you will need the 6dB rule otherwise if no exponent is involved then you will need the 3dB rule. For example power is the 3dB because no square is used, but pressure uses a square so the 6dB rule is used when it is doubled.

Suppose we have doubled the pressure in the room from .01 Pa to .02 Pa, this will give a 6dB SPL increase. If we increased again from .02 Pa to .04 Pa we would again only increase by 6dB SPL!

Plus or minus 6db SPL correlates to a doubling or halving distance since distance is affected by the inverse square law. As sound travels it spreads out according to this law.

Example

As a quick example, say I have a microphone 2 meters in front of a sound source. I then move the microphone to 4 meters away. Since the distance doubled and assuming I am in a free field (meaning sound propagates in all directions with no loss to thermal energy or any other parasitic force) then I expect the SPL to decrease by 6dB SPL. Likewise, if I moved the mic to 1 meter then an increase in 6dB SPL is expected. This is why rules in multi-micing a single sound source exist. If two mics on the same source are too close, then large phasing and other issues can occur.

Converting from Dynes to dB SPL

Knowing the threshold of human hearing is:

.00002 Pa or .0002 dyncm2 .00002\ Pa\ or\ .0002\ \frac{dyn}{cm^{2}}
, we can easily convert a number of dynes to pascals.

Consider the fact that they both represent the same thing, the threshold of hearing. So if we put the threshold of hearing over the threshold of hearing then we have the number 1.

1=threshold of hearingthreshold of hearing=.00002 Pa.0002dyncm2=.1Padyncm2 1=\frac{threshold\ of\ hearing}{threshold\ of\ hearing} =\frac{.00002\ Pa}{.0002\frac{dyn}{cm^{2}}} =.1\frac{Pa}{\frac{dyn}{cm^{2}}}

Plugging in the values for the units shows that we can simply multiply by .1 to go from dynes per centimeter squared to pascals or divide by .1 to go to dynes per centimeter squared to pascals.

Example

Convert

90dyncm2 90\frac{dyn}{cm^{2}}
to pascals.

If we multiply by a form of 1 we do not change the number because anything times 1 is itself. So we use our trick from above. We know a form of 1 is:

.00002 Pa.0002dyncm2 \frac{.00002\ Pa}{.0002\frac{dyn}{cm^{2}}}
so we can multiply by this without changing the fraction. Note because the top and bottom of the fraction are the same thing, the threshold of hearing, we can place which ever one we need on top and on bottom. The are interchangeable because they are both the threshold of hearing. We want to cancel dynes per centimeter squared so we choose to put that on the bottom. This gives:

90dyncm2×.00002 Pa.0002 dyncm2 90\frac{dyn}{cm^{2}} \times \frac{.00002\ Pa}{.0002\ \frac{dyn}{cm^{2}}}

The dynes per centimeter squared simplify out to 1 and we are left with our answer in pascals:

9 Pa 9\ Pa

Note that we could have just multiplied by .1 directly to go to pascals but I wanted to show why we could do that. If we want to go from pascals to dynes per centimeter squared we could do so by the same process which would work out as dividing by .1. Be sure you always include your units!

Example

Now say you are asked to convert

90dyncm2 90\frac{dyn}{cm^{2}}
to dB SPL.

Here we have a few options. We will need to use the dB SPL equation but with what reference? The simplest option is to use the reference we are already in. In this case dynes per centimeter squared. Our second option it to convert to a reference we would like to use instead. If we wanted to use the pascals reference instead then we would need to convert first to pascals and then use the dB SPL equation with the pascal reference. Lets do the easy thing and just use the reference we already have. This gives:

dBSPL=20log⁡(90dyncm2.0002dyncm2)≈113 dBSPL dB_{SPL} =20\log\left(\frac{90\frac{dyn}{cm^{2}}}{.0002\frac{dyn}{cm^{2}}}\right) \approx 113\ dB_{SPL}

Try converting to pascals and finding the dB SPL. You will find you get the same answer.

Example

Convert

2 Pa 2 \ Pa
to dB SPL.

Solution

dBSPL=20log⁡(2 Pa.00002 Pa)=100 dBSPL dB_{SPL} =20\log\left(\frac{2\ Pa}{.00002\ Pa}\right) = 100\ dB_{SPL}

Questions

  1. If the dBSPL is increased by 10 by what factor did the intensity increase?

  2. Convert

    35dyncm2 35\frac{dyn}{cm^{2}}
    to dB SPL.

  3. Convert

    35dyncm2 35\frac{dyn}{cm^{2}}
    to dB SPL but first convert to Pascals.

  4. Convert

    35 Pa 35 \ Pa
    to dB SPL.

  5. Why is the answer for pascals bigger?

  6. If we quintupled in the input do we expect the dB SPL to also quintuple? Why?

To support this series please consider donating via

paypal

or joining the

patreon.

© 2012-2023 Composing Gloves

Terms and Conditions

Contact